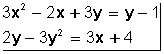
forman un sistema de dos ecuaciones con dos incógnitas .
El conjunto de ecuaciones:
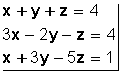
forman un sistema de tres ecuaciones con tres incógnitas.
Se llama grado del sistema de ecuaciones al mayor exponente al que se encuentre elevada alguna incógnita del sistema.
Por ejemplo,
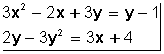
es un sistema de dos ecuaciones con dos incógnitas de segundo grado, porque el mayor exponente es 2 (la x e y al cuadrado). Este sistema con ecuaciones de segundo grado se llaman tambiénsistema de ecuaciones cuadráticas .
El sistema de ecuaciones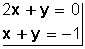
es de primer grado con dos incógnitas (porque todos los valores están elevados a 1, que no se escribe).
El sistema de ecuaciones
es de primer grado con dos incógnitas (porque todos los valores están elevados a 1, que no se escribe).
Cuando el sistema de ecuaciones es de primer grado y además no aparecen términos con las incógnitas multiplicadas entre sí (tipo x • y) se dice que es un sistema de ecuaciones lineales .
Resolviendo sistemas
Para resolver un sistema de ecuaciones existen los siguientes métodos:
Método de sustitución
Lo que debemos hacer:
1.- Despejar una de las incógnitas en una de las ecuaciones.
2.- Sustituir la expresión obtenida en la otra ecuación.
3.- Resolver la ecuación resultante.
4.- Calcular la otra incógnita en la ecuación despejada.
Ejemplo:
Resolver
Se despeja x en la segunda ecuación:
x = 8 – 2y
Se sustituyen en la primera ecuación:
3(8 – 2y) – 4y = – 6
Operando:
24 − 6y − 4y = − 6
24 – 10y = – 6
− 10y = − 6 − 24
− 10y = − 30
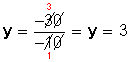
Se resuelve:
y = 3
Se sustituye este valor en la segunda:
x + 2(3) = 8
x + 6 = 8
x = 8 – 6 = 2
Solución del sistema:
x = 2, y = 3
Método de reducción
Lo que debemos hacer:
1.- Se igualan los coeficientes de una incógnita, salvo el signo, eligiendo un múltiplo común de ambos.
2.- Puede ser el producto de los coeficientes de esa incógnita.
3.- Se suman o restan, según convenga, las ecuaciones.
4.- Se resuelve la ecuación de primer grado resultante.
5.- Se calcula la otra incógnita sustituyendo el valor obtenido en una de las ecuaciones del sistema.
Ejemplo:
Resolver
Primero se deben igualar el 6 y el 8 de la incógnita x . Para hacerlo, amplificamos la primera ecuación por 4 y amplificamos la segunda ecuación por –3. Esto porque al multiplicar 6x por 4 queda 24x; y al multiplicar 8x por –3 queda –24x, y se anulan entre sí; o sea, hemos eliminado una incógnita para trabajar solo con la otra (la y ). Luego hacemos lo mismo con la y .
Se elimina la x :  |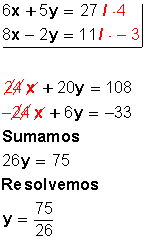
Se elimina la y :
 |
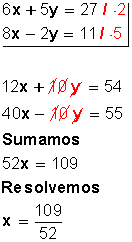Método de igualación
Lo que debemos hacer:
1.- Se despeja una de las incógnitas en ambas ecuaciones.
2.- Se igualan las expresiones, con lo que obtenemos una ecuación con una incógnita.
3.- Se resuelve la ecuación resultante.
4.- El valor obtenido se sustituye en cualquiera de las dos expresiones en las que aparecía despejada la otra incógnita.
5.- Los dos valores obtenidos constituyen la solución del sistema.
Ejemplo:
Resolver
Despejamos x en la primera ecuación:
Despejamos x en la segunda ecuación:
x = –1 – 2y
Igualamos ambas expresiones:
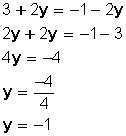
:Se sustituye este valor en la primera o segunda ecuación:
x = 3 + 2(−1)
x = 3 − 2
x = 1
Solución del sistema:
x = 1, y = –1
Otro ejemplo:
Resolver, por el método de igualación, el sistema
Despejamos , por ejemplo, la incógnita x de la primera y segunda ecuación:
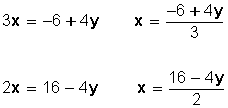
Igualamos ambas expresiones:
Luego, resolvemos la ecuación:
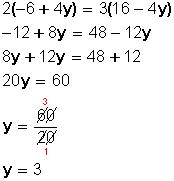
Sustituimos el valor de y , en una de las dos expresiones en las que tenemos despejada la x :
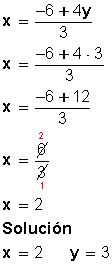
Ver, en Youtube:
Fuente Internet:
