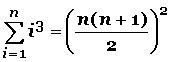La operación sumatoria se expresa con la letra griega sigma mayúscula Σ, y se representa así:

Expresión que se lee: " sumatoria de Xi, donde i toma los valores desde 1 hasta n ".
i es el valor inicial, llamado límite inferior.
n es el valor final, llamado límite superior.
Pero necesariamente debe cumplirse que:
i ≤ n
Si la sumatoria abarca la totalidad de los valores, entonces no se anotan sus límites y su expresión se puede simplificar:
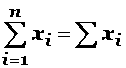
Ahora, veamos un ejemplo:
Si se quiere expresar la suma de los cinco primeros números naturales se puede hacer de esta forma:
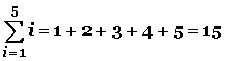
Pero también hay fórmulas para calcular los sumatorios más rápido.
Una anécdota aclaratoria
La historia relata que cuando Carl Friedrich Gauss tenía diez años su profesor de matemática le impuso al curso, como una forma de mantenerlos ocupados por largo rato, el siguiente ejercicio:
Sumar todos los números desde el 1 hasta el 100, de este modo:
1 + 2+ 3 + 4 + 5 + 6 + 7 + 8 + 9 + ……………….+ 98 + 99 + 100 =
Confiado en que los niños estarían ocupados durante mucho rato, el profesor se enfrascó en sus tareas de estudio, pero a los cinco minutos, el pequeño Gauss le entregó el resultado: 5.050.
Sorprendido, el profesor le pidió a Gauss que le explicara cómo lo hizo:
El pequeño se dio cuenta de que la suma del primer número con el último (1 + 100 = 101) da un resultado que se repite sumando todos los simétricos: 1 + 100 = 101; 2 + 99 = 101; 3 + 98 = 101; 4 + 97 = 101; etc., logrando establecer 50 sumas cuyo resultado es 101.
Entonces, hizo: 50 veces 101 es igual a 50 x 101 = 5.050
Este procedimiento nos conduce a la fórmula de la sumatoria de n números consecutivos:
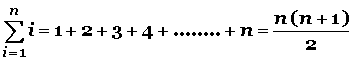
Si aplicamos la fórmula al problema anterior, tendremos:
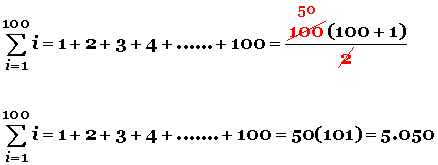
Por ejemplo, para sumar los primeros mil números naturales no tiene mucho sentido sumar número por número, si se puede usar la fórmula:
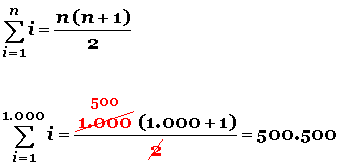
Algunas fórmulas de la operación sumatoria
Fórmula para la suma de n números consecutivos (1+ 2 + 3 + 4 + 5 ……+ n); que acabamos de ver arriba.
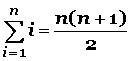
Fórmula para la sumatoria de los cuadrados de n números consecutivos (1 2 + 2 2 + 3 2 + 4 2 + 5 2 + 6 2 + ……….+ n 2 ) :
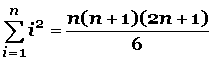
Fórmula para la sumatoria de los cubos de n números consecutivos (1 3 + 2 3 + 3 3 + 4 3 + 5 3 + 6 3 + 7 3 ……..+ n 3 ):