Razones Iiteradas o Serie de Razones

Como ya vimos, una razón es una comparación entre dos cantidades. Puede expresarse como fracción, como división o como par ordenado pero independientemente de cómo se escriba, la razón compara cantidades .

Por ejemplo, si en curso hay 12 mujeres y 24 hombres, se puede comparar la cantidad de hombres y mujeres. Dicha comparación puede expresarse como:

Si la razón es 2 : 1 significa  que por cada 2 hombres hay 1 mujer (por cada 4 hombres hay 2 mujeres; por cada 6 hombres hay 3 mujeres, etc)

Ahora bien, si se igualan tres o más razones del mismo valor, se establecen una serie de razones o razones iteradas .

Donde k es la constante de proporcionalidad .

Por lo tanto, se puede escribir:

a : b : c = d : e : f

o bien

La clave para conocer o despejar valores desconocidos en una serie de razones o razones iteradas, está en la siguiente regla: la suma de los antecedentes (equivale a los numeradores) es a la suma de los consecuentes (equivale a los denominadores) como un antecedente (un denominador) cualquiera es al consecuente (denominador) respectivo.

Expresado en forma matemática esto es:

Ejercicios:

1.- Sea 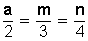 , hallar a , m y n sabiendo que a + m + n = 36 
Sabemos que la suma de los antecedentes (numeradores) es a la suma de los consecuentes (denominadores)  como cada antecedente es a cada consecuente.

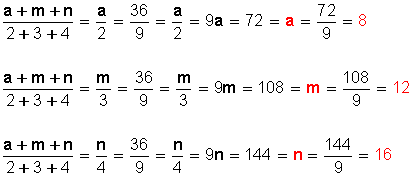
Respuesta:  a = 8; m = 12  y n = 16 .

2.-  Sea 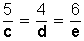 , hallar c, d y e, sabiendo que c + d + e = 120

Hacemos

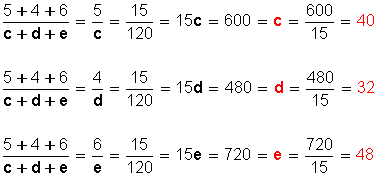
Respuesta:  c = 40; d = 32  y e = 48 .

Resolver:

3.- Sea 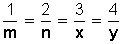 , hallar m, n, x e y, sabiendo que m + n + x + y = 14

4.- Tenemos tres números cuya suma es 240 , y ellos guardan entre sí la relación de los números 2, 3 y 5. ¿Cuáles son esos tres números?