Dicha comparación podría indicarse como una razón, en cuatro formas distintas, de este modo:
1.- a:b
2.- a ÷ b
3.-
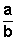
4.- La razón de a es a b.
2.- a ÷ b
3.-
4.- La razón de a es a b.
 |
Así, la razón de 8 a 4 se puede escribir:
8 : 4
8÷4
Razón de 8 a 4
De modo general, podemos decir que: Una razón es un cuociente entre dos cantidades . El valor de ese cuociente se llama valor de la razón.
Si se tiene dos cantidades a y b , se dice “a es a b” y se escribe .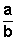
Al término “a” le llamamos antecedente y al término “b” le llamamos consecuente .
Si se tiene dos cantidades a y b , se dice “a es a b” y se escribe
.Al término “a” le llamamos antecedente y al término “b” le llamamos consecuente .
Ejemplo:
Así, en la razón 8 ÷ 4 , el antecedente es 8 y el consecuente 4.
Hay que tener presente que las comparaciones por medio de una razón se hacen en unidades del mismo tipo. Por ejemplo, para expresar la relación entre 6 m y 30 cm ambas cantidades deben expresarse en la misma unidad. Entonces, la forma apropiada para esta relación es 600 cm : 30 cm, no 6m: 30 cm.
Ejemplos
1.- Suponga que en un curso hay 13 hombres y 25 mujeres. Entonces “la razón” entre hombres y mujeres del curso es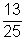 
se lee “13 es a 25”
se lee “13 es a 25”
2.- En una caja hay 5 bolas rojas y 7 verdes. La razón entre las bolas verdes y las bolas rojas es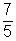 
, se lee “7 es a 5”
, se lee “7 es a 5”Propiedades de las razones
Como vemos en los ejemplos, debido a que la razón de dos cantidades no es más que una división indicada o una fracción, las propiedades de las razones serán las propiedades de las fracciones o quebrados.
1) Si el antecedente (equivale al numerador) de una razón se multiplica o divide por un número, la razón queda multiplicada o dividida por ese número.
2) Si el consecuente (equivale al denominador) de una razón se multiplica o divide por un número, la razón queda divida en el primer caso y multiplicada en el segundo por ese mismo número.
3) Si el antecedente y el consecuente de una razón se multiplican o dividen por un mismo número, la razón no varía .
De acuerdo con estas propiedades, los términos pueden reducirse o aumentarse, simplificarse, etcétera.
 |
Por ejemplo, para reducir la razón 15 : 20 a los términos de menor valor se escribe la razón como una fracción y luego se procede como éstas.
Entonces, 15 : 20 se transforma en
Y se lee 15 es a 20 como 3 es a 4.
Por tanto, la razón de 15:20 es la misma que la razón de 3:4.
Razón inversa
Con frecuencia es útil comparar los números de una razón en el orden inverso. Para hacer esto simplemente intercambiamos el numerador y el denominador. Entonces, la inversa de 15:20 es 20:15.
Cuando los términos de una razón se intercambian resulta una razón inversa .
Practicar con razones
Escriba las siguientes razones como una fracción y reduzca a los términos de menor valor.
1.- La razón de 5 kg a 15 kg
2.- $ 16 : $12
3.- 16 ÷ 4
4.- 1 mililitro a 1 centílitro
5.- 5x a 10x
6.- 
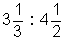
Escriba la inversa de las siguientes razones:
7.- La razón de 6m a 18 m
8.- 
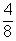
9.- 5 : 8
10.- 15 a 21
11. Hallar la razón de:
a) 60 y 12
b)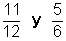 
c) 5:6 y 3:5
d) 3/8 y 0,02
12. Hallar la relación entre las edades de dos niños de 10 y 14 años.
13. Cite tres pares de números que estén en la relación de 2 y 3.
14. Cite tres pares de números cuya razón sea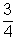 
.
15. Cite tres pares de números cuya relación sea de 1 a 6.
.15. Cite tres pares de números cuya relación sea de 1 a 6.
16. La razón de dos números es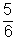 
. Si el menor es 20, ¿Cuál es el mayor?
17. El mayor de dos números es 42 y la relación entre ambos es de 5 a 7. Hallar el número menor.
. Si el menor es 20, ¿Cuál es el mayor?17. El mayor de dos números es 42 y la relación entre ambos es de 5 a 7. Hallar el número menor.
18. Dos números son entre sí como 2 es a 17. Si el menor es 14, ¿cuál es el mayor?
 |
Respuestas
 |
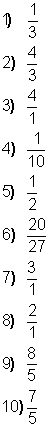
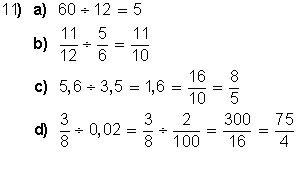
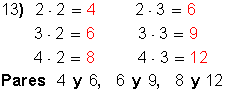
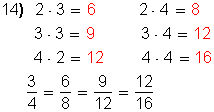
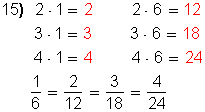
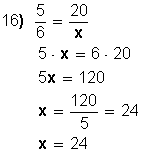
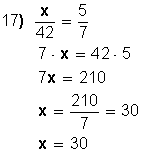
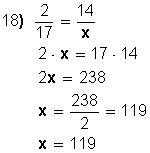
Proporción
Íntimamente ligado al estudio de las razones está el tema de la proporción .
Una proporción no es más que una ecuación en la cual los miembros son razones. En otras palabras, cuando dos razones se igualan una a otra se forma una proporción.
La proporción podrá escribirse en tres formas diferentes:
15 : 20 : : 3 : 4
15 : 20 = 3 : 4
Las dos últimas formas son las más comunes. Todas estas formas se leen "15 es a 20 como 3 es a 4", En otras palabras, 15 tiene la misma relación con 20 que 3 la tiene con 4.
Un aspecto de la extrema importancia de las proporciones es que si se dan tres términos el cuarto podrá determinarse resolviendo una simple ecuación.
Es evidente, de la observación de la última forma, 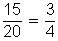, que una proporción es una ecuación fraccionaria. Por tanto, todas las reglas para las ecuaciones fraccionarias (en Q) se aplican aquí.
, que una proporción es una ecuación fraccionaria. Por tanto, todas las reglas para las ecuaciones fraccionarias (en Q) se aplican aquí.
Fuentes Internet:
