Suma de matrices
Para sumar dos matrices, ambas tienen que tener las mismas dimensiones.
Para sumar dos matrices se suman los elementos que ocupan las mismas posiciones.
Ejemplo:
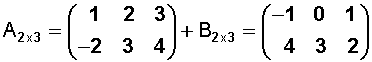
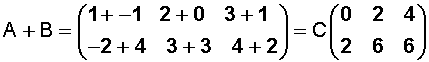
Propiedades de la suma de matrices
Propiedad asociativa: A + (B + C) = (A + B) + C
Propiedad conmutativa: A + B = B + A
Propiedad del elemento neutro: A + 0 = A (0 es la matriz nula)
Propiedad del elemento simétrico: La matriz –A, que se obtiene cambiando de signo todos los elementos de A, recibe el nombre de matriz opuesta de A.
Producto de una matriz por un número cualquiera
Para multiplicar un número cualquiera por una matriz se multiplica el número por todos los elementos de la matriz, obteniéndose otra matriz del mismo orden.
Ejemplo:
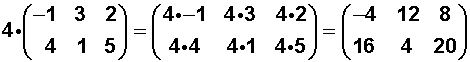
Propiedades del producto de una matriz por un número cualquiera (k)
Propiedad distributiva (1ª): k (A + B) = k A + k B
Propiedad distributiva (2ª): (k + h) A = k A + h A (h = número cualquiera)
Propiedad asociativa mixta: k [h A] = (k h) A
Propiedad del elemento unidad: 1· A = A (1 por A = A)
Producto de matrices
Para multiplicar dos matrices es indispensable que el número de columnas de la primera matriz sea igual al número de filas de la segunda matriz.
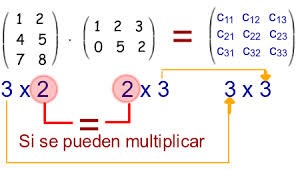
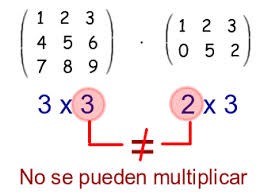
Dadas dos matrices:
A = (a ij ) m×n y B = (b ij ) p×q
donde n = p , es decir, el número de columnas de la primera matriz A es igual al número de filas de la matriz B, se define el producto A·B de la siguiente forma:
El elemento que ocupa el lugar (i, j) en la matriz producto se obtiene sumando los productos de cada elemento de la fila i de la matriz A por el correspondiente de la columna j de la matriz B.
Ejemplo:
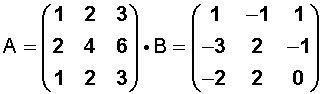
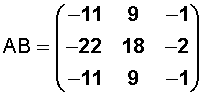
Desarrollado sería así:
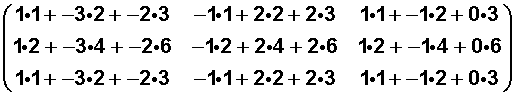
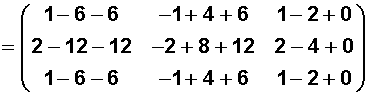
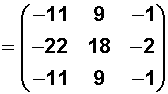
Para entender y no equivocarse, veamos una manera graficada de saber cómo obtenemos el -11:
Hacemos un cuadro con la primera fila de A (1, 2, 3) y la primera columna de B (1, -3, -2)
1
|
2
|
3
|
x
|
1
|
1
| ||
-6
|
-3
| ||
-6
|
-2
|
Multiplicamos el primer elemento de la primera fila por el primer elemento de la primera columna (1 x 1); luego, multiplicamos el segundo elemento de la primera fila por el segundo elemento de la primera columna (2 x -3), y luego multiplicamos el tercer elemento de la primera fila por el tercer elemento de la primera columna (3 x -2).
Los colores indican las multiplicaciones:
1 x 1 = 1;
2 x -3 = -6;
3 x -2 = -6
1 x 1 = 1;
2 x -3 = -6;
3 x -2 = -6
Y luego sumamos los productos: 1 +(-6) + (-6) = 1 – 6 – 6 = 1 – 12 = -11
Veamos cómo se obtiene el 9:
Hacemos un cuadro con la primera fila de A y la segunda columna de B
1
|
2
|
3
|
x
|
-1
|
-1
| ||
4
|
2
| ||
6
|
2
|
Multiplicamos el primer elemento de la primera fila por el primer elemento de la segunda columna (1 x -1); luego, multiplicamos el segundo elemento de la primera fila por el segundo elemento de la segunda columna (2 x 2), y luego multiplicamos el tercer elemento de la primera fila por el tercer elemento de la segunda columna (3 x 2).
Los colores indican las multiplicaciones:
1 x -1 = -1;
2 x 2 = 4;
3 x 2 = 6
2 x 2 = 4;
3 x 2 = 6
Sumamos los productos: -1 + 4 + 6 = 9
Veamos ahora cómo se obtiene el –1:
Hacemos un cuadro con la primera fila de A y la tercera columna de B
1
|
2
|
3
|
x
|
1
|
1
| ||
-2
|
-1
| ||
0
|
0
|
Seguimos el mismo predicamento de multiplicaciones y luego sumamos los productos: 1 + (-2) + 0 = 1 – 2 + 0 = -1
Y seguimos así:
Un cuadro con la segunda fila de A y la primera columna de B
Un cuadro con la segunda fila de A y la segunda columna de B
Un cuadro con la segunda fila de A y la tercera columna de B
Un cuadro con la tercera fila de A y la primera columna de B
Un cuadro con la tercera fila de A y la segunda columna de B
Un cuadro con la tercera fila de A y la tercera columna de B
Propiedades del producto de matrices
Propiedad: A·(B·C) = (A·B)·C
El producto de matrices en general no es conmutativo.
Si A es una matriz cuadrada de orden n se tiene A·In = In·A = A.
Dada una matriz cuadrada A de orden n, no siempre existe otra matriz B tal que A·B = B·A = In. Si existe dicha matriz B, se dice que es la matriz inversa de A y se representa por A–1.
El producto de matrices es distributivo respecto de la suma de matrices, es decir: A·(B + C) = A·B + A·C
Fuentes Internet:






