Ejercicio 1)
Dada la ecuación exponencial
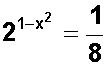
Para resolverla, primero expresamos el denominador de la fracción (el segundo elemento de la ecuación) como potencia de 2 :
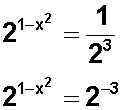
Y vemos que la fracción con exponente positivo en el denominador se convirtió en una base entera con exponente negativo.
Esto en virtud de la siguiente propiedad de las potencias :
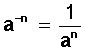
Esta propiedad indica que toda potencia con exponente negativo es igual al inverso de su base, ahora con exponente positivo en el denominador, lo cual funciona en ambos sentidos.
Ahora, siendo iguales las bases, los exponentes también deben ser iguales:
Entonces, la ecuación para igualar los exponentes queda:
1 – x 2 = –3
Y resolvemos esta ecuación
–x 2 = –3 –1
–x 2 = – 4 /* –1
x 2 = 4
x = √4
x = ± 2
Ejercicio 2)
Dada la ecuación
Si usamos una propiedad de las potencias (multiplicación de potencias de igual base y distinto exponente), esta ecuación puede expresarse así:
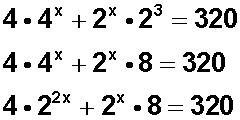
En ecuaciones como esta es necesario hacer un cambio de variable para su resolución.
Aquí podemos usar 2 x como nueva variable llamada y , entonces tendremos que
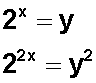
Hacemos los reemplazos correspondientes para obtener
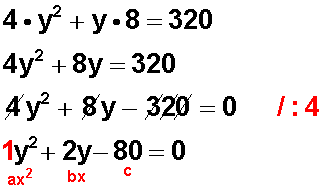
Lo agregado en rojo es solo ilustrativo para entender la aplicación de la fórmula general.
Entonces, tenemos una ecuación de segundo grado o cuadrática que es afín con la fórmula general,
ax2 + bx + c = 0
Y para resolver esta última utilizamos la fórmula general para resolver ecuaciones de segundo grado :
La recordamos:
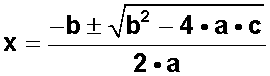
Reemplazamos la x por una y , en seguida ponemos los valores que nos entrega la ecuación anterior:
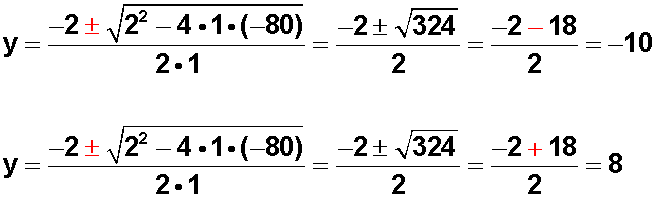
Ahora, retrocedemos y deshacemos el cambio de variable
y = 2 x
Si
y = 2 x vale –10
no habrá solución para la ecuación inicial, ya que 2 x siempre es positivo.
En cambio si
y = 2 x vale 8, x valdrá 3, ya que 2 3 = 8
La solución es, por tanto,
x = 3
Ver: Resolución de ecuaciones de primer grado
Ver en youtube






