Ejercicio 1)
Dada la ecuación exponencial
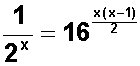
Para resolverla, sabemos que tenemos que igualar las bases ; pero la primera tarea será convertir la fracción del primer término en un entero .
Para hacerlo, usamos una de las propiedades de las potencias (potencias con exponente entero negativo) .
En nuestro caso:
Si en el primer término tenemos la fracción con numerador UNO y el denominador como potencia, podemos ir a la potencia con exponente entero negativo, y viceversa.
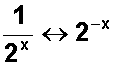
Y ahora tenemos una base 2 en el primer término y luego podremos igualar las bases, convirtiendo el 16 del segundo término en 2 4

Además, en el segundo término, potencia de potencia , se multiplican los exponentes (otra propiedad de las potencias) y simplificamos lo que se pueda.
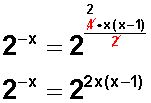
Ahora resolvemos. Tenemos una ecuación exponencial, con potencias de igual base ; por lo tanto, si las bases son iguales, obligatoriamente los exponentes también deben ser iguales (propiedad de las potencias) :
Entonces, tenemos los exponentes de ambos términos:
Y resolvemos
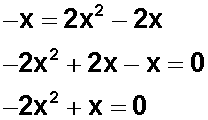
Así llegamos a una ecuación de segundo grado incompleta , la cual resolvemos sacando factor común (que es x) .
Nos queda un producto que es igual a cero. Si un producto es igual a cero, necesariamente uno de sus factores será igual a cero (Teorema del Factor Nulo) .
Entonces, usemos el factor
(—2x + 1) = 0
Y hacemos
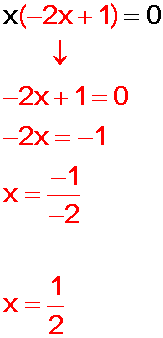
Ejercicio 2)
Sea la ecuación
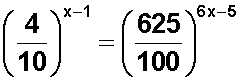
Para resolverla, debemos igualar las bases ; pero lo primero será simplificar las fracciones :
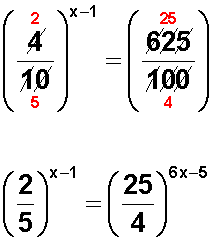
Ahora trataremos de igualar las bases, y para ello convertimos en potencias el numerador y el denominador del segundo miembro :
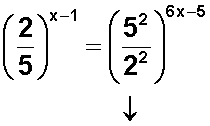
Aplicamos otra propiedad de las potencias: División de potencias con el mismo exponente (dicho de otro modo, fracciones con el mismo exponente tanto en el numerador como en el denominador), la fracción se eleva al exponente común :
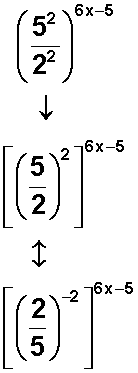
En el segundo paso anterior, aplicamos otra propiedad de las potencias: toda potencia de exponente entero positivo se convierten en su inverso con el mismo exponente, pero negativo (conversión que se puede hacer en ambos sentidos) .
Así los

Ahora podemos reescribir la ecuación inicial, la que tenemos ya con bases iguales:
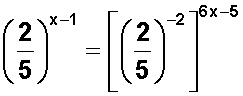
En el segundo miembro nos encontramos con potencia sobre potencia , entonces (otra propiedad de las potencias) los exponentes se multiplican .
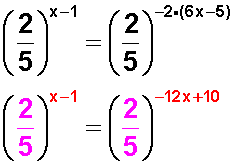
Y llegamos a la clave: si tenemos una ecuación exponencial cuyos miembros tienen la misma base, obligatoriamente sus exponentes deben ser iguales:
Entonces, igualamos los exponentes:
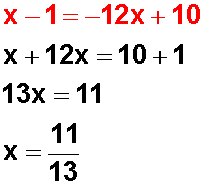
Ejercicio 3)
Dada la ecuación
Recordemos que tenemos que intentar igualar las bases; para llegar a ello debemos usar varias estrategias según lo que tengamos a la vista:
En este caso, no podemos hacer nada todavía con las bases, pero vemos que hay algo en común en los exponentes: aparece una incógnita (la x); entonces, trabajemos con los exponentes:
En el primer miembro, tenemos
Si recordamos las propiedades de las potencias, deberíamos recordar esto:
(Multiplicación de potencias de igual base y distinto exponente, se conserva la base y se suman los exponentes)
Entonces, podemos hacer
Ahora tenemos en el 2 2x una multiplicación en el exponente (2 por x), lo cual nos recuerda que una potencia de potencia se resuelve manteniendo la base y multiplicando los exponentes:
La generalización dice que
(a n ) m = a n . m
Entonces podemos expresarlo así:
(2 x ) 2 • 4 = 9 • 2 x – 2
Recién visualizamos algo en común en las bases: el 2 x , entonces recurrimos a una estrategia llamada “cambio de variable”, y este 2 x lo reemplazaremos por U ,
Para expresar nuestra ecuación como
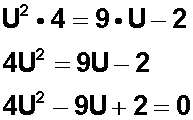
La que igualando a cero hemos convertido en una ecuación de segundo grado o cuadrática , de la forma que conocemos (se supone que debemos conocer: ax 2 + bx + c = 0 ):
La práctica nos diría que podemos factorizar este trinomio para obtener el producto de dos binomios con un término común , pero aquí hay un elemento que es esencial: el coeficiente principal (llamado también líder) es distinto de 1 (uno), en este caso es 4 (cuatro). Y cuando el coeficiente principal de la ecuación es mayor que 1, la factorización no resulta.
Para solucionar este entuerto, la regla dice que antes de proceder a factorizar (o expresar un polinomio como producto de sus factores) un polinomio cuyo coeficiente principal es mayor que 1 (uno) debemos multiplicar el polinomio por su coeficiente principal, y a la vez dividirlo por el mismo para que la factorización sea correcta:
En nuestro caso, debemos multiplicar el polinomio por 4 y dividirlo por 4, ya que 4 es el coeficiente principal del polinomio:
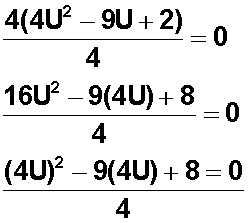
Ahora podemos buscar dos binomios que tengan un término en común (en este caso U) y formados con dos números que sumados entre sí den −9 y multiplicados entre sí den +8: esos números serán −8 y −1:
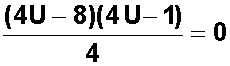
Ahora vemos si alguno de los componentes de los binomios tiene factor común. Vemos que hay factor común en (4U – 8); entonces
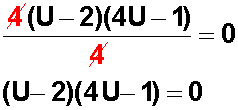
Esto nos queda luego de simplificar por 4, entonces podemos aplicar el Teorema del Factor Nulo , el cual nos dice que si un producto es igual a cero, uno de los factores de dicho producto será igual a cero.
Según esto, tenemos dos opciones:
Si U – 2 = 0, entonces U = 2
Si 4U − 1 = 0, entonces 4U = 1 y U = 1/4
Pero aquí debemos recordar que U = 2 x , por lo tanto debemos cambiar de nuevo la variable.
Para el primer caso, anotamos
2 x = 2, o 2 x = 2 1 ,
entonces si hay potencias de igual base, serán iguales sus exponentes:
Así x = 1
Para el segundo caso, anotamos
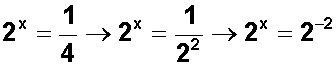
Así x = –2
La respuesta sería que
x = {−2 ; 1},
se anota entre corchetes el valor de ambas soluciones, anotando primero la menor de ellas.





