Usado en operaciones matemáticas, podríamos definirlo como las cifras que son consideradas relevantes para el cálculo en una operación.
Las cifras no significativas aparecen formando parte en el resultado de los cálculos y no se las considera, son nulas.
Se dice que las cifras significativas de un número son determinadas por su margen de error . ¿Qué significa esto?
Veamos un ejemplo:
Tenemos el número Pi = 3,141516….., una cifra con infinitos decimales en la cual siempre el último dígito señala un error, ya que es imposible determinar su valor en forma exacta.
Entonces que hacemos generalmente, tomamos solo 3 cifras significativas y usamos siempre 3,14 como valor de Pi, dejando todo el resto como cifras no significativas.
El margen de error en los cálculos con Pi será menor si usamos más cifras significativas; o sea, si usamos más decimales. Por ejemplo, si usamos 3,141516 como valor para Pi.
Ahora, usadas en el campo físico, especialmente en mediciones instrumentales, las cifras significativas están dadas por los propios instrumentos.
Expliquemos esto:
Al medir cualquier magnitud, siempre se comenten errores. Pero no sólo se cometen al leer los datos de los instrumentos de medida, sino que también en los resultados de operaciones aritméticas en las que se vean involucrados números decimales.
Al realizar una medición con un instrumento, este nos devuelve un valor formado por una serie de cifras. Dicha serie de cifras recibe el nombre de cifras significativas.
Entonces, se denominan cifras significativas al conjunto de los dígitos que se conocen con seguridad en una medida.
De todas las cifras significativas siempre hay una, la última, que estará afectada por un error, como ya vimos con el ejemplo de Pi. Por esta razón, al resto de cifras, las que se consideran, se las denomina cifras exactas .
Tomemos como ejemplo los datos o valores que nos entrega un termómetro digital:
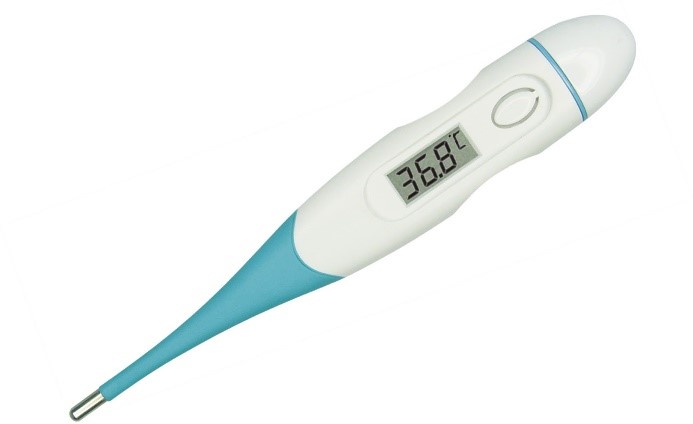 |
Los termómetros digitales usados en medicina utilizan 3 cifras significativas. Las dos primeras son cifras exactas y la última es una cifra significativa afectada por error ya que probablemente la temperatura real estará formada por infinitos decimales imposibles de representar y que además no son necesarios para determinar si el paciente tiene fiebre o no.
El termómetro de la figura indica una temperatura de 36,8 grados, aunque puede ser de 36,81324546 grados.
Reglas para el cómputo de las cifras significativas
Ahora bien, estas consideraciones tanto matemáticas como físicas, nos conducen a las siguientes reglas para el cómputo de cifras significativas, generalmente, aunque no universalmente, admitidas:
1.- Todas las cifras diferentes de cero que expresen cantidades iguales o superiores al margen de error, son significativas.
(3,141592... ± 0,002) mm, será 3,142, con 4 cifras significativas (a partir de 592… no son significativas)
± 0,002 significa que se considera una cifra con un margen de error de ± 2 milésimas de mm, por ello es que el número es 3,142, con 4 cifras significativas (más adelante veremos por qué es 3,142 y no 3,141).
(3,141592... ± 0,0007) mm, será 3,1416, con 5 cifras significativas (a partir de 92… no son significativas)
A la hora de contar el número de cifras exactas o significativas no se tienen en cuenta los ceros que están a la izquierda de la primera cifra no nula.
Número
|
Cifras significativas
|
(3,141592... ± 0,0001) mm
|
5 (3,1416)
|
(0,041592... ± 0,0001) mm
|
3 (0,0416) (se lee: 416 diez milésimas)
|
2.- Todos los ceros entre dígitos significativos son significativos.
| Número |
Cifras significativas
|
7.053
|
4
|
7053
|
4
|
302
|
3
|
3.- Los ceros a la izquierda del primer dígito que no es cero sirven solamente para fijar la posición del punto decimal y no son significativos.
| Número |
Cifras significativas
|
0,0056
|
2 (se lee: 56 diez milésimas)
|
0,0789
|
3 (se lee: 789 diez milésimas)
|
0,000001
|
1 (se lee: una millonésima)
|
4.- En un número con dígitos a la derecha de la coma decimal, los ceros a la derecha del último número diferente de cero son significativos.
Número
|
Cifras significativas
|
43
|
2
|
43,00
|
4 (se lee 43 coma cero cero)
|
0,00200
|
3 (se lee 200 cien milésimas)
|
0,40050
|
5 (se lee 40050 cien milésimas)
|
5.- En un número que no tiene coma decimal y que termina con uno o más ceros (como 3600), los ceros con los cuales termina el número pueden ser o no significativos. El número es ambiguo en términos de cifras significativas.
En este caso, para especificar el número de cifras significativas, se requiere información adicional acerca de cómo se obtuvo el número. Si el número es el resultado de una medición, los ceros probablemente no son significativos. Si el número es resultado de una operación matemática, todos los dígitos son significativos.
Se evitan confusiones expresando los números en notación científica . Cuando están expresados en esta forma, todos los dígitos se interpretan como significativos.
Número
|
Cifras significativas
|
3,6 x 105
|
2
|
3,60 x 105
|
3
|
3,600 x 105
|
4
|
2 x 105
|
1
|
2,0 x 105
|
2
|
Reglas de operaciones con cifras significativas
Cuando se ejecutan operaciones matemáticas que involucren cifras significativas, o se deban entregar resultados de mediciones físicas, se deben cumplir las siguientes reglas:
Regla 1: Los resultados experimentales se expresan con sólo una cifra dudosa, e indicando con ± la incertidumbre en la medida.
Regla 2: Las cifras significativas se cuentan de izquierda a derecha, a partir del primer dígito diferente de cero y hasta el dígito dudoso.
Regla 3: Al sumar o restar dos números decimales, el número de cifras decimales del resultado es igual al de la cantidad con el mayor número de ellas.
Atención:
Hay casos especiales en la resta. Citemos el siguiente ejemplo:
30,3475 – 30,3472 = 0,0003
Vemos que cada una de las cantidades tiene seis cifras significativas y el resultado posee tan solo una. En este caso, al restar se han perdido cifras significativas. Esto es importante tenerlo en cuenta cuando se trabaja con calculadoras o computadores en donde haya cifras que se sumen y se resten. Es conveniente realizar primero las sumas y luego las restas para perder el menor número de cifras significativas posible.
Regla 4: Al multiplicar o dividir dos números, el número de cifras significativas del resultado es igual al del factor con menos cifras significativas.
Ejemplo:
Si multiplicamos 3,21 x 3,817 = 12,25257, debemos usar solo 12,3 como resultado (3 cifras significativas con un solo decimal, ya que manda el 3,21, que tiene 3 cifras significativas).
Y aquí aparece un nuevo concepto. Como vemos, para mantener la cantidad de cifras significativas, el 25257 del resultado lo expresamos como 3. ¿Qué hicimos? Redondeamos el resultado.
Redondeo
Un concepto o práctica matemática que está asociado al concepto de cifra significativa es el concepto de Redondeo .
Cuando realizamos algún tipo de operación matemática resulta muy práctico reducir el número de decimales que obtenemos para evitar trabajar con valores excesivamente grandes. El redondeo ayuda a que los resultados sean lo más precisos posibles.
Se denomina redondeo al proceso de eliminar las cifras situadas a la derecha de la última cifra significativa.
Reglas para el redondeo
Cuando el primero de los dígitos descartados es cinco o mayor que cinco, la cifra anterior se aumenta en una unidad.
Ejemplo: 45,367892 redondeado a 4 cifras significativas, queda como 45,37. Debido a que para dejar 4 cifras, hay que descartar desde la quinta en adelante; es decir, desde el 7. Y 7 es mayor que 5 por lo que aumentamos en una unidad la anterior. Por tanto es: 45,37
Cuando el primero de los dígitos descartados es menor que cinco, la cifra anterior se mantiene igual.
Ejemplo: 123,643421 redondeado a 5 cifras significativas queda como 123,64. Debido a que para dejar 5 cifras, hay que descartar desde la sexta en adelante; es decir, desde el 3. Y 3 es menor que 5 por lo que la cifra anterior la dejamos igual. Por tanto es: 123,64
Cuando realizamos operaciones matemáticas con valores decimales, el resultado debe redondearse hasta un número determinado de cifras significativas.
Cuando sumamos o restamos, el resultado debe tener el mismo número de decimales que el valor que más tenga:
Ejemplo: 12,07 + 3,2 = 15,27
Cuando multiplicamos o dividimos, el resultado debe tener el mismo número de cifras significativas que el valor que tenga menos de ellas:
Ejemplo: 12,07 x 3,2 = 39 (No se coloca 38,624 ya que 3,2 tiene 2 cifras significativas)
Nota:
Se recomienda revisar el tema Estimación matemática , donde hay más sobre el redondeo.
Fuentes Internet:






