Los ejercicios deben desarrollarse de acuerdo a las operatorias que se realicen. Se pueden restar o sumar términos semejantes, multiplicar expresiones algebraicas o bien simplificarlas.
Símbolos y términos específicos
Entre los símbolos algebraicos se encuentran números, letras y signos que representan las diversas operaciones aritméticas.
Los números son, por supuesto, constantes, pero las letras pueden representar tanto constantes como variables. Las primeras letras del alfabeto se usan para representar constantes y las últimas para variables.
Operaciones y agrupación de símbolos
La agrupación de los símbolos algebraicos y la secuencia de las operaciones aritméticas se basa en los símbolos o signos de agrupación , que garantizan la claridad de lectura del lenguaje algebraico.
Entre los símbolos de agrupación se encuentran los paréntesis ( ), corchetes [ ], llaves { } y rayas horizontales —también llamadas vínculos— que suelen usarse para representar la división y las raíces, como en el siguiente ejemplo:
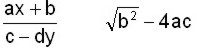
Los símbolos de las operaciones básicas son bien conocidos de la aritmética: adición (+), sustracción (-), multiplicación (×) y división (:).
En el caso de la multiplicación, el signo ‘×’ normalmente se omite o se sustituye por un punto, como en a · b. Un grupo de símbolos contiguos, como abc, representa el producto de a, b y c.
La división se indica normalmente mediante rayas horizontales. Una raya oblicua, o virgulilla, también se usa para separar el numerador, a la izquierda de la raya, del denominador, a la derecha, en las fracciones.
Hay que tener cuidado de agrupar los términos apropiadamente.
Por ejemplo, ax + b/c - dy indica que ax y dy son términos separados, lo mismo que b/c, mientras que ( ax + b )/( c – dy ) representa la fracción:
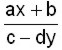
Prioridad de las operaciones
Cada expresión algebráica (y matemática) posee una estructura estrictamente jerarquizada.
Esto significa que para resolver una expresión algebraica es necesario seguir un orden establecido con el fin de garantizar que los cálculos tengan sólo un resultado.
Ese orden es el siguiente:
1) Cuando no hay signos de agrupación (paréntesis, corchetes, llaves) hacemos primero las multiplicaciones y divisiones si las hay. Si hay varios números positivos y negativos los agrupamos y después los sumamos.
2) Si hay signos de agrupación (paréntesis, corchetes, llaves) se realizan en primer lugar todas las operaciones que se encuentren dentro de ellos, respetando la secuencia general.
Los símbolos de agrupación indican el orden en que se han de realizar las operaciones: se hacen primero todas las operaciones dentro de un mismo grupo, comenzando por el más interno.
Cuando hay paréntesis y corchetes, hacemos primero los paréntesis, los quitamos aplicando la regla de los signos . Después hacemos los corchetes y los quitamos aplicando la regla de los signos (recuerden que la regla de los signos se aplica solo para multiplicaciones y divisiones).
3) Luego se efectúan las elevaciones a potencia y las raíces (potencias y raíces tienen la misma jerarquía)
4) En seguida se resuelven las multiplicaciones y las divisiones (multiplicaciones y divisiones tienen la misma jerarquía)
5) Finalmente se realizan las sumas y las restas (sumas y restas tienen la misma jerarquía)
Cuando un conjunto de operaciones se encuentran en el mismo nivel de prioridad o jerarquía, las operaciones se realizan desde la izquierda hacia la derecha.
Por ejemplo:
Ver en Youtube:
Un importante error conceptual relacionado con el significado del signo igual
Es común que muchos estudiantes consideren el signo = solo como una invitación al cálculo y no como una relación de equivalencia.
Así, por ejemplo, interpretan la expresión
5 + 8 = x + 3
en términos similares a los siguientes: “A 5 se le suma 8 y al resultado (x) se le suma 3”.
Por tal razón, consideran que x debe valer 13 y piensan que la expresión debería completarse así:
5 + 8 = x + 3 = 16
Como dijimos, este es un error muy común. Es importante, en este sentido, hacer notar desde un comienzo que el signo igual indica que todo los que está a la izquierda del signo igual (en este caso, 5 + 8) representa la misma cantidad que lo que está a su derecha (en este caso, x + 3). Para que ello se cumpla, x debe valer 10.
Gran parte de las dificultades que encuentran los estudiantes tienen su origen en este error conceptual.
Números Reales
Los números que se utilizan en el álgebra son los números reales . Hay un número real en cada punto de la recta numérica.
Los números reales se dividen en números racionales, números irracionales y números enteros , los cuales a su vez se dividen en números negativos, números positivos y cero (0) .
Podemos verlo en esta tabla:
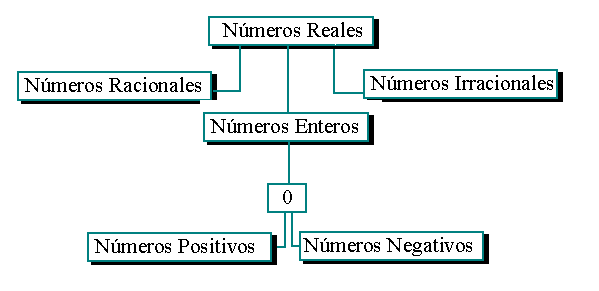
Un número real es racional si se puede representar como cociente a/b , donde a sea un entero y b sea un entero no igual a cero. Los números racionales pueden escribirse en forma decimal.
Existen dos maneras para hacerlo:
1) como decimales finitos
2) como decimales que se repiten infinitamente
Los números reales que no pueden ser expresados en la forma a/b , donde a y b son enteros se llaman números irracionales . Los números irracionales no tienen decimales finales ni decimales que se repiten infinitamente.
Al hacer operaciones algebraicas, se asume que se cumplen las mismas propiedades que para la aritmética numérica.
En aritmética, los números usados son sólo del conjunto de los números racionales. La aritmética, por sí sola, no puede ir más lejos, pero el álgebra y la geometría pueden incluir números irracionales, como la raíz cuadrada de 2 y números complejos.
Repitiendo el concepto, el conjunto de todos los números racionales e irracionales constituye el conjunto de los números reales.
Propiedades de los números reales
Propiedades de la adición
La suma de dos números reales a y b cualesquiera dará como resultado otro número real que se escribe a + b . Los números reales son uniformes para las operaciones de adición, sustracción, multiplicación y división; esto quiere decir que al realizar una de estas operaciones con números reales el resultado es otro número real.
Propiedad Asociativa de la adición :
Cualquiera que sea la forma en que se agrupan los términos de la adición, el resultado de la suma es siempre el mismo: ( a + b ) + c = a + ( b + c ).
También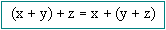 
Es la llamada propiedad asociativa de la adición.
Es la llamada propiedad asociativa de la adición.
Un ejemplo aritmético: (4 + 2) + 9 = 4 + (2 + 9)
Elemento neutro de la adición
Dado un número real a cualquiera, existe el número real cero (0) conocido como elemento neutro de la adición,
tal que a + 0 = 0 + a = a.
Elemento simétrico de la adición
Dado un número real a cualquiera, existe otro número real (- a ), llamado elemento simétrico de a (o elemento recíproco de la suma), tal que a + (- a ) = 0.
Propiedad Conmutativa de la adición
Cualquiera que sea el orden en que se realiza la operación, la suma es siempre la misma: a + b = b + a.
También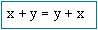 
Es la llamada propiedad conmutativa de la adición.
Es la llamada propiedad conmutativa de la adición.
Un ejemplo aritmético: 4 + 2 = 2 + 4
Propiedades de la multiplicación
Para la multiplicación se cumplen propiedades similares a las de la adición. Sin embargo, en la multiplicación hay que prestar especial atención al elemento neutro y al elemento recíproco o inverso.
El producto de dos números reales a y b es otro número real, que se escribe a·b o ab.
Propiedad Asociativa de la multiplicación
Cualquiera que sea la forma de agrupar los términos de la multiplicación, el producto es siempre el mismo: ( ab ) c = a ( bc ).
También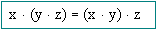 
Es la llamada propiedad asociativa de la multiplicación.
Es la llamada propiedad asociativa de la multiplicación.
Un ejemplo aritmético: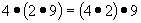 
Elemento neutro
Dado un número real a cualquiera, existe el número real uno (1) llamado elemento neutro de la multiplicación,
tal que a (1) = 1( a ) = a.
Elemento recíproco o inverso
Dado un número real a distinto de cero, existe otro número ( a –1 o 1/a ), llamado elemento inverso (o elemento recíproco de la multiplicación), para el que a(a –1) = (a –1 ) a = 1.
Propiedad Conmutativa de la multiplicación
Cualquiera que sea el orden en que se realiza la multiplicación, el producto es siempre el mismo: ab = ba.
También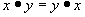 
Es la llamada propiedad conmutativa de la multiplicación.
Es la llamada propiedad conmutativa de la multiplicación.
Un ejemplo aritmético: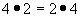 
Propiedad distributiva de multiplicación sobre adición:
Otra propiedad importante del conjunto de los números reales relaciona la adición y la multiplicación de la forma siguiente:
a ( b + c ) = ab + ac también ( b + c ) a = ba + ca
También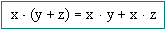 
Un ejemplo aritmético: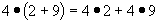 
Regla de los Signos para sumar y restar:
1. En una suma de números con signos iguales, se suman los números y el resultado lleva el mismo signo. Si los números tienen signos diferentes, se restan y el resultado lleva el signo del mayor.
Ejemplo:
5 + 8 = 13
5 + –8 = –3
2. En resta de signos iguales el resultado lleva el signo del mayor. Si se restan signos diferentes, se suman los números y el resultado lleva el signo del mayor.
Ejemplo:
5 – 8 = –3
5 – (–8) = 13
Regla de los signos en la multiplicación y la división
En multiplicación y división de números con signos iguales el resultado es positivo. Si los números son de signos opuestos, el resultado es negativo.
Ejemplos:
5 x 8 = 40 5 x –8 = –40
Multiplicación de polinomios
El siguiente ejemplo es el producto de un monomio por un binomio:
(ax + b) (cx 2 ) = acx 3 + bcx 2
Este mismo principio —multiplicar cada término del primer polinomio por cada uno del segundo— se puede ampliar directamente a polinomios con cualquier número de términos. Por ejemplo, el producto de un binomio y un trinomio se hace de la siguiente manera:
(ax 3 + bx 2 – cx) (dx + e) = adx 4 +aex 3 + bdx 3 + bex 2 – cdx 2 - cex
Una vez hechas estas operaciones, todos los términos de un mismo grado se han de agrupar, siempre que sea posible, para simplificar la expresión:
= adx 4 + (ae + bd)x 3 + (be – cd) x 2 – cex
Recta Numérica
Para construir una recta numérica , primero se escoge un punto en la recta que será un punto arbitrario al que le llamaremos cero (0). Este punto es llamado el origen de la recta numérica.
El origen separa la recta en dos partes, el lado positivo y el lado negativo. A la derecha del origen está el lado positivo y el negativo está a la izquierda. En el lado derecho van números enteros positivos (en orden sucesivo) y en el lado izquierdo se escriben los números enteros negativos (en orden sucesivo), estos se marcan en unidades equidistantes.
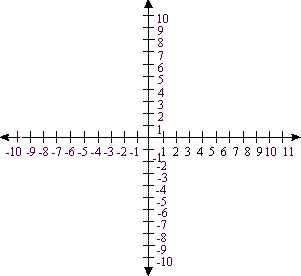
Es importante recordar que para cualesquiera dos números reales diferentes a los que llamaremos a y b , siempre uno es mayor que el otro.
· Si a – b es positivo, entonces a > b.
· Si b – a es positivo, entonces a < b.
Valor Absoluto
La distancia de un número en la recta numérica desde cero (0) se llama valor absoluto . Se representa con el símbolo |x|. El valor absoluto de un número se calcula de la siguiente manera:
· si el número es negativo, lo convertimos a positivo.
· si el número es cero o positivo, se queda igual.
Ejemplos:
|7| = 7
|–7| = 7
Notación Exponencial
La notación exponencial se usa para repetir multiplicaciones de un mismo número. Es la elevación a la enésima potencia (n) de una base (X).
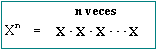
Ejemplos:
x 2 = x · x
2 2 = 2 · 2
3 4 = 3 · 3 · 3 · 3
Término algebraico
Término algebraico es el producto de una o más variables y una constante numérica o literal.
Ej:
7xy 3
–2mnp 2
π r 2
En todo término algebraico hay:
Signo: positivo o negativo
Coeficiente numérico: es el número que va al comienzo del término algebraico
Factor literal: son las letras y sus exponentes
Grado: corresponde al mayor exponente dentro de los términos
Término algebraico
|
Signo
|
Coeficiente numérico
|
Factor literal
|
Grado
|
2m 2 n 5
|
Positivo
|
2
|
m 2 n 5
|
5
|
5 a 3 b 6 c 8
|
Positivo
|
5
|
a 3 b 6 c 8
|
8
|
- 1/3 zhk 5
|
Negativo
|
1/3
|
zhk 5
|
5
|
Expresiones Algebraicas
Expresión algebraica es el resultado de combinar, mediante la operación de adición, uno o más términos algebraicos.
Las expresiones algebraicas se clasifican según su número de términos.
monomio = un solo término.
Por ejemplo: 3x 2
binomio = suma o resta de dos monomios.
Por ejemplo: 3x 2 + 2x
trinomio = suma o resta de tres monomios.
Por ejemplo: 3x 2 + 2x – 5
polinomio = suma o resta de cualquier número de monomios.
Monomio
|
Binomio
|
Trinomio
|
Polinomio
|
8 x 3 y 4
|
3 a 2 b 3 + 8z
|
a – b 9 + a 3 b 6
|
2/3 a 2 + bc + a 2 b 4 c 6 – 2
|
x 2
|
z 5 +32 x 3
|
9a – b 2 + c 3
|
ab – a 6 b 3 c + 8 – 26a
|
Ver: Reglas de los Exponentes
Productos Notables
1. 
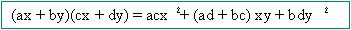
Por ejemplo:
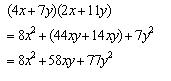
2. 
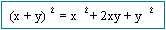
3. 
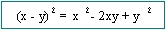
4. 
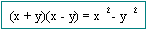
5. 
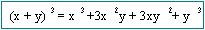
6. 
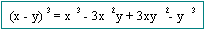
7. 
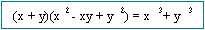
8. 
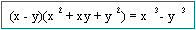
Expresiones fraccionales
Una fracción es una expresión en la forma:
Una expresión fraccional está simplificada cuando el numerador y el denominador no tienen factores comunes.
Por ejemplo:
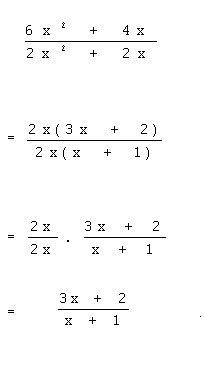
Multiplicación de expresiones algebraicas
Para multiplicar expresiones fraccionales, se multiplican los numeradores y se multiplican los denominadores.
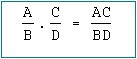
Por ejemplo:
Para dividir se multiplica por el recíproco y luego se factoriza y se simplifica el resultado.
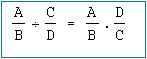
Por ejemplo:
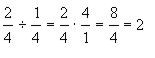
Suma y resta de expresiones algebraicas
En suma y resta cuando los denominadores son los mismos, se suman o restan los numeradores y se mantiene el mismo denominador.
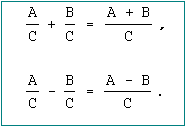
Por ejemplo:
Exponentes enteros
Reglas básicas para trabajar los exponentes:
Regla:
|
Ejemplo:
|
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |
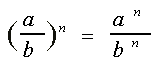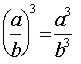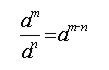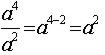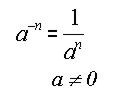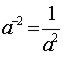Radicales (Raíces)
Un radical es una expresión en la forma:
que se lee "raíz n de b"
Cada parte de un radical lleva su nombre,
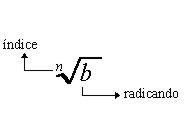
El índice debe ser un entero positivo. Para una raíz cuadrada, el índice 2 es usualmente omitido.
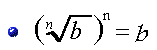
Ejemplo:
Ejemplo:
Ejemplo:
Ejemplo:
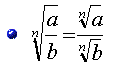
Ejemplo:
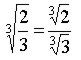
Suma y Resta de Radicales (de raíces)
Cuando tenemos radicales "semejantes", podemos resolver la suma o la resta usando la propiedad distributiva y agrupando los términos semejantes. Los radicales "semejantes" son los que tienen el mismo radicando.
Ejemplos:
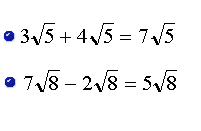
Si los radicales no son semejantes, la suma o la resta sólo puede ser indicada. Se puede agrupar los términos semejantes del radical.
Ejemplo:
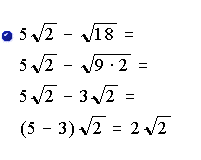
Fuentes Internet:
