Entre tantas operaciones algebraicas encontramos la división de polinomios . Y, entre ellas, tenemos el caso específico de dividir un polinomio entre un binomio .
Cuando un polinomio es dividido entre un binomio, generalmente hay un residuo.
Y el teorema del residuo establece que si un polinomio de x, f(x) , se divide entre (x – a) , donde a es cualquier número real o complejo, entonces el residuo es f(a) .
Esto significa que para encontrar el residuo cuando un polinomio es dividido entre un binomio el valor de x es igual al valor a, o f(x) = f(a) .
En estos casos, debemos calcular entonces el valor de x, que será igual al de a.
Considere el polinomio x 2 – 8 x + 6 , el cual podemos identificar como una función polinomial f( x ) = x 2 – 8 x + 6 .
Dividamos este polinomio entre el binomio x – 2 , para ver si hay un residuo:
Podemos realizar la división en cualquier método.
Método 1: División larga
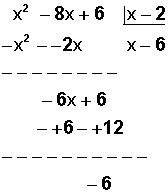
El residuo es -6.
Método 2: División sintética
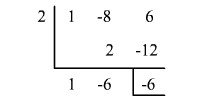
El residuo es –6.
Método 3. Usando el teorema del residuo
f ( x ) = x 2 – 8 x + 6 dividido entre x – 2,
para calcular el valor de x, hacemos x – 2 = 0
x = 2
y por el teorema sabemos que x = a , y lo reemplazamos en el polinomio dividendo:
2 2 – 8 (2) + 6 y resolvemos
4 – 16 + 6 = –6 (mismo residuo que obtuvimos en las formas anteriores de dividir un polinomio entre un binomio)






