Razón y proporción numérica
Razón entre dos números
Siempre que hablemos de Razón entre dos números nos estaremos refiriendo al cociente (el resultado de dividirlos) entre ellos.
Entonces:
Razón entre dos números a y b es el cociente entre
|
Por ejemplo, la razón entre 10 y 2 es 5 , ya que
|
Y la razón entre los números 0,15 y 0,3 es
|
Proporción numérica
Ahora, cuando se nos presentan dos razones para ser comparadas entre sí, para ver como se comportan entre ellas, estaremos hablando de una proporción numérica.
Entonces:
| Los números a, b, c y d forman una proporción si la razón entre a y b es la misma que entre c y d . | |
Es decir
| |
| Se lee “ a es a b como c es a d” | |
Los números 2, 5 y 8, 20 forman una proporción, ya que la razón entre 2 y 5 es la misma que la razón entre 8 y 20.
Es decir
|
| En la proporción | hay cuatro términos; a y d se llaman extremos , c y b se llaman medios. |
La propiedad fundamental de las proporciones es: en toda proporción, el producto de los extremos es igual al de los medios.
|
Así, en la proporción anterior
|
se cumple que el producto de los extremos nos da 2 x 20 = 40 y el producto de los medios nos da 5 x 8 = 40
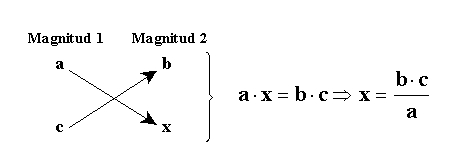
Comprendido el concepto de proporción como una relación entre números o magnitudes, ahora veremos que esa relación puede darse en dos sentidos:
Las dos magnitudes pueden subir o bajar (aumentar o disminuir) o bien si una de las magnitudes sube la otra bajo y viceversa.
Si ocurre, como en el primer caso, que las dos magnitudes que se comparan o relacionan pueden subir o bajar en igual cantidad, hablaremos de Magnitudes directamente proporcionales .
Si ocurre como en el segundo caso, en que si una magnitud sube la otra baja en la misma cantidad, hablaremos de Magnitudes inversamente proporcionales .
MAGNITUDES DIRECTAMENTE PROPORCIONALES
Si dos magnitudes son tales que a doble, triple... cantidad de la primera corresponde doble, triple... cantidad de la segunda, entonces se dice que esas magnitudes son directamente proporcionales .
|
Ejemplo
Un saco de papas pesa 20 kg. ¿Cuánto pesan 2 sacos?
Un cargamento de papas pesa 520 kg ¿Cuántos sacos de 20 kg se podrán hacer?
Número de sacos
|
1
|
2
|
3
|
...
|
26
|
...
|
Peso en kg
|
20
|
40
|
60
|
...
|
520
|
...
|
Para pasar de la 1ª fila a la 2ª basta multiplicar por 20
Para pasar de la 2ª fila a la 1ª dividimos por 20
Observa que
|
Las magnitudes número de sacos y peso en kg son directamente proporcionales .
La constante de proporcionalidad para pasar de número de sacos a kg es 20.
Esta manera de funcionar de las proporciones nos permite adentrarnos en lo que llamaremos Regla de tres y que nos servirá para resolver un gran cantidad de problemas matemáticos.






