Para un período determinado sería
Capital final (C f ) = capital inicial (C) más los intereses.
Veamos si podemos generalizarlo con un ejemplo:
Hagamos cálculos para saber el monto final de un depósito inicial de $ 1.000.000, a 5 años plazo con un interés compuesto de 10 % (como no se especifica, se subentiende que es 10 % anual).
| Año |
Depósito inicial
|
Interés
|
Saldo final
|
0 (inicio)
|
$1.000.000
|
($1.000.000 x 10% = ) $100.000
|
$1.100.000
|
1
|
$1.100.000
|
($1.100.000 × 10% = ) $110.000
|
$1.210.000
|
2
|
$1.210.000
|
($1.210.000× 10% = ) $121.000
|
$1.331.000
|
3
|
$1.331.000
|
($1.331.000 × 10% = ) $133.100
|
$1.464.100
|
4
|
$1.464.100
|
($1.464.100 × 10% = ) $146.410
|
$1.610.510
|
5
|
$1.610.510
|
Paso a paso resulta fácil calcular el interés sobre el depósito inicial y sumarlo para que esa suma sea el nuevo depósito inicial al empezar el segundo año, y así sucesivamente hasta llegar al monto final.
Resulta simple, pero hay muchos cálculos; para evitarlos usaremos una fórmula de tipo general:
En inversiones a interés compuesto, el capital final (C f ) , que se obtiene a partir de un capital inicial (C) , a una tasa de interés (i) , en un tiempo (t) , está dado por la fórmula:
Recordemos que i se expresa en forma decimal ya que corresponde a 
.
Y donde t corresponde al número de años durante los cuales se mantiene el depósito o se paga una deuda.
.Y donde t corresponde al número de años durante los cuales se mantiene el depósito o se paga una deuda.
Como corolario a esta fórmula:
A partir de ella, puesto que el interés compuesto final (I) es la diferencia entre el capital final y el inicial, podríamos calcular la tasa de interés (i) :
Sacamos factor común C:
También podemos calcular la tasa de interés despejando en la fórmula de C f :
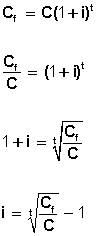
En los problemas de interés compuesto i y t deben expresarse en la misma unidad de tiempo efectuando las conversiones apropiadas cuando estas variables correspondan a diferentes períodos de tiempo.
Periodos de interés compuesto
El interés compuesto no se calcula siempre por año, puede ser semestral, trimestral, al mes, al día, etc. ¡Pero si no es anual debería informarse!
Así, si la fórmula del interés compuesto se ha deducido para una tasa de interés anual durante t años, todo sigue siendo válido si los periodos de conversión son semestres, trimestres, días, etc., solo hay que convertir éstos a años.
Por ejemplo, si i se expresa en tasa anual y su aplicación como interés compuesto se valida en forma mensual , en ese caso i debe dividirse por 12
. En seguida, la potencia t (el número de años) debe multiplicarse por 12 para mantener la unidad mensual de tiempo (12 meses por el número de años).
debe dividirse por 12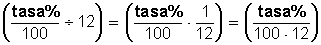 . En seguida, la potencia t (el número de años) debe multiplicarse por 12 para mantener la unidad mensual de tiempo (12 meses por el número de años).
Si los periodos de conversión son semestrales, i se divide por 2 ya que el año tiene dos semestres (lo cual significa que los años los hemos convertido a semestres), por lo mismo, luego habrá que multiplicar la potencia t (el número de años) por 2 (el número de semestres de un año):
Suponiendo una tasa anual de 10%, hacemos del siguiente modo:
será igual a
Si los periodos de conversión son trimestrales, i se divide por 4 ya que el año tiene 4 trimestres (lo cual significa que los años los hemos convertido a trimestres) por lo mismo, luego habrá que multiplicar la potencia t (el número de años) por 4 (el número de trimestres que hay en un año).
Del siguiente modo:
será igual a
En general, en todos los casos donde haya que convertir a semestres, trimestres, meses, o días se multiplica por n semestres, trimestres, meses o días el 100 de la fórmula 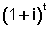que es igual a
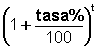. La potencia t (en número de años) se debe multiplicar por el mismo valor de n , en cada caso, así, suponiendo una tasa anual de 10%:
que es igual a . La potencia t (en número de años) se debe multiplicar por el mismo valor de n , en cada caso, así, suponiendo una tasa anual de 10%: será igual a
Fuentes Internet:
