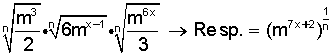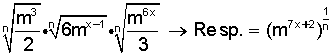Ejercicios con Radicales

Aprendido o repasado todo sobre las raíces practicaremos con ellas con algunos ejercicios o problemas que se nos presenten:

Ejercicio 1

Se nos pide resolver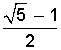 

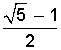
Como no hay instrucciones en cuanto a la forma o método para resolverlo, debemos tener presente que:

a) no se puede extraer raíz (5 es número primo)

b) no se pueden restar los términos porque no son términos semejantes

c) no se puede dividir porque no hay términos que sean múltiplos

Esta expresión se puede racionalizar ; es decir, se puede amplificar por un factor adecuado que permita transformar el numerador irracional en un número racional.

La fracción se puede amplificar por el número 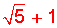 porque al multiplicarlo por el numerador se obtiene el producto notable llamado suma por diferencia:

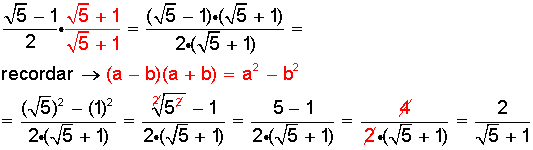
Ejercicio 2

Se nos pide calcular raíz de equis al cuadrado (x 2 ) menos y al cuadrado (y 2 ) , por raíz de equis (x) menos y (todo sin paréntesis).

Expresado en forma matemática, nos queda:

Recordemos la propiedad de las raíces acerca de la multiplicación de raíces de igual índice :

Se multiplican las bases y se conserva el índice.

Entonces, hacemos:

Aquí podemos ver que la primera expresión dentro de la raíz corresponde a un producto notable ( suma por diferencia ), que ya vimos y que podemos factorizar, cuya fórmula es:

Entonces, factorizamos esa primera expresión:

Antes de multiplicar los términos entre sí los reordenamos y podemos ver que hay un cuadrado del binomio :

Entonces, nuestra expresión queda:

Aplicamos la misma propiedad anterior, pero ahora en sentido inverso y nos queda:

En seguida, aplicamos otra de las propiedades de raíces:

Para extraer la raíz de una potencia cuyo exponente es igual al índice, de la forma 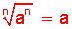 , exponente e índice se anulan entre sí, por lo tanto desaparece el radical  y la base queda aislada. Dicho de otro modo, exponente e índice, iguales, se simplifican, y desaparece el signo radical:

Lo que no deja la expresión final del siguiente modo:

   

Ejercicios para resolver

1) 

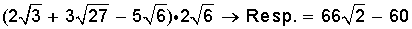
2) 

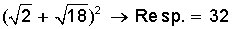
3) 

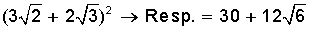
4) 

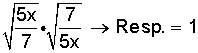
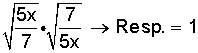
5) 

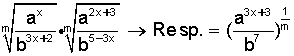
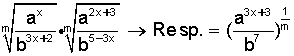
6)