(Números racionales o fraccionarios)
Una ecuación en el conjunto de los Números Racionales (Q) contiene fracciones positivas o negativas o bien números decimales . También pueden participar Números Enteros que se pueden transformar en fracciones simplemente dividiéndolas por 1
Ejemplo: —3 = —3 /1
La idea de resolver una ecuación, tal como se ha dicho (Ver “ Resolución de ecuaciones. Método general ”), es encontrar el valor de la incógnita “x” para que la igualdad sea verdadera.
Debe tenerse presente que si los denominadores son diferentes deben igualarse, tal como se hace cuando se suman o restan fracciones, sacando el Mínimo Común Múltiplo (M.C.M.) .
Ejemplo: La siguiente ecuación pertenece a los Números Racionales porque sus coeficientes numéricos son fracciones; es decir, son números que tienen la forma: 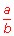
En esta ecuación los denominadores son diferentes (4, 2 y 3), por lo tanto, deben igualarse para poder realizar las operaciones de suma o resta (Recuerde: sólo se suman o restan fracciones de igual denominador) . Para lograr esto se busca el Mínimo Común Múltiplo (m.c.m.).
El mínimo común múltiplo entre dos o más números corresponde al número más pequeño divisible por cada uno de los denominadores que se dan.
Existen varios métodos para encontrarlo, pero uno de los más fáciles y rápidos es el de la tabla de números primos. (En ella se anotan todos los denominadores de las fracciones que se desean sumar o restar y se dividen todos ellos por números primos: 2, 3, 5, 7, 11, 13, 17, etc.
Estas operaciones se terminan hasta que todos los números terminan en 1, luego se multiplican los números primos que aparecen más veces y que se obtuvieron al dividir los denominadores.
Un número primo es el que tiene como factores el 1 y el mismo número. Ej: el 2 es número primo por que los únicos números que al multiplicarse dan 2, son el 1 y el 2 : 2 · 1 = 2.
Ahora se debe ver cuántas veces cabe cada denominador de las fracciones de la ecuación en el mínimo común múltiplo (m. c. m.) hallado mediante la tabla de factores primos (12); el resultado de cada uno de ellos se debe multiplicar por el numerador respectivo. Concretamente: el denominador 4 de la fracción 3 / 4 cabe en el 12 tres veces, ahora se debe multiplicar el numerador (que es 3) por 3, y así sucesivamente.
Ahora que todos los denominadores están iguales se suprimen , y se trabaja con la parte de arriba y se resuelve como una ecuación en Z.
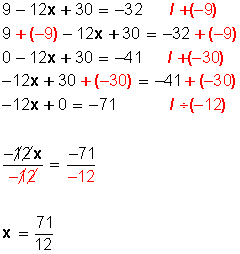
Ahora sólo falta practicar, todas las veces que sea necesario, con constancia y empeño.






