Un polinomio se puede dividir por un monomio o por otro polinomio.
La operación es muy similar a la división tradicional de números, donde hay un divisor, un dividendo, un cociente y un resto.
Dividir un polinomio se ve más complejo por la inclusión de términos algebraicos que tienen letras y números.
Por ello, para explicar la división de polinomios desarrollaremos un ejercicio práctico:
Vamos a dividir el polinomio
(6x 5 + x 4 + 4x 2 – 7x + 1) entre (2x 2 + x – 3)
Primero, ordenamos tanto el dividendo como el divisor de mayor a menor según sus grados, y completamos el grado que falte:
(6x 5 + x 4 + 0x 3 + 4x 2 – 7x + 1) entre (2x 2 + x – 3)
En el dividendo agregamos 0x 3 ya que ese grado faltaba.
Ahora, el polinomio, que es el dividendo, lo colocamos a la izquierda, y el divisor lo ponemos enmarcado a la derecha:
Dividimos el primer monomio del dividendo (+6x 5 ) entre el primer monomio del divisor (+2x 2 ).
+6x 5 : +2x 2 = +3x 3
Este resultado (+3x 3 ) lo ponemos debajo de la caja y lo multiplicamos por cada término del polinomio divisor y el resultado lo vamos restando en el polinomio dividendo:
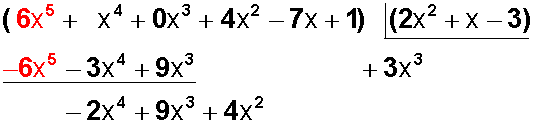
Aquí debemos tener cuidado: al multiplicar +3x 3 , primero por +2x 2 ; luego por + x y luego por -3, hay que tener en cuenta la regla de los signos, y el resultado que pongamos abajo en el dividendo debe llevar signo contrario al obtenido.
Bajamos el monomio siguiente (+4x 2 ) y continuamos:
Ahora dividimos -2x 4 : +2x 2 = -x 2
Y este resultado lo agregamos al cociente y lo multiplicamos por +2x 2 , luego por +x y luego por -3:
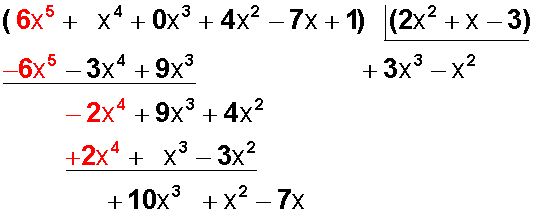
Bajamos e monomio siguiente (-7x),
y ahora dividimos +10x 3 : + 2x 2 = + 5x
Y +5 x lo agregamos al cociente, lo multiplicamos por +2x 2 , luego por+ x y luego por -3:
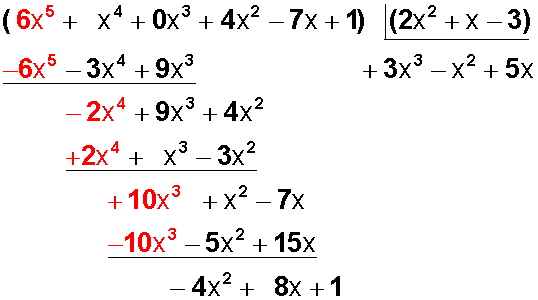
Bajamos el último monomio (+1),
y ahora dividimos -4x 2 : +2x 2 =-2
-2 lo agregamos al cociente y repetimos la operación anterior:
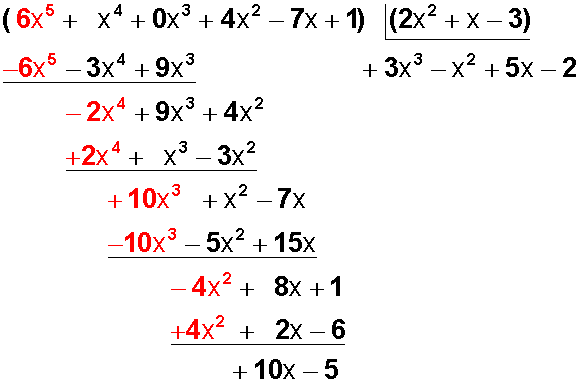
Ahora no queda nada más por bajar en el dividendo y si el grado del resto (+10x) es menor que el grado del divisor (2x 2 ), hemos terminado la división.
Cociente o resultado: +3x 3 – x 2 + 5x -2
Resto: +10x -5
Ver: en youtube una explicación pormenorizada






