Veámoslo con diferentes ejemplos:
Simplificar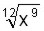 
Un radical se puede expresar como una potencia de exponente fraccionario .
En nuestro ejemplo, se puede expresar como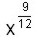
.
En nuestro ejemplo, se puede expresar como
.
Por tanto se puede simplificar igual que una fracción; o sea se divide el índice (12 que se coloca como denominador) y el exponente (9 que se coloca como numerador) por un mismo número. (9 y 12 son divisibles por 3, y quedan como 3 y 4)
Ahora podemos hacer el camino inverso y una potencia con exponente fraccionario como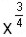 
podemos expresarla como un radical 
.
podemos expresarla como un radical .
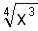También se puede simplificar directamente (cuando es posible), dividiendo el índice y el exponente por un mismo número (12 ÷ 3 = 4 y 9 ÷ 3 = 3).
Otros casos y más ejemplos:
Simplificar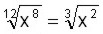 
Simplificamos directamente dividiendo, en este caso, índice y exponente entre 4.
Simplificar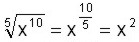 
Expresamos el radical como una potencia con exponente fraccionario y simplificamos la fracción.
Simplificar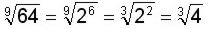 
Factorizamos la base (64 = 2 x 2 x 2 x 2 x 2 x 2 = 2 6 ), luego dividimos el índice (9) y el exponente (6) por 3 y desarrollamos el cuadrado de la base (4).
Simplificar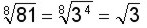 
Factorizamos la base (81 = 3 x 3 x 3 x 3 = 3 4 ), luego dividimos el índice (8) y el exponente (4) por 2, quedando como índice 2 (que no se escribe) y la base como 3l cuyo exponente (1) tampoco se escribe.
Simplificar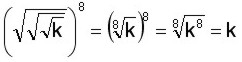 
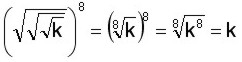
Para calcular la raíz de una raíz se multiplican los índices de las raíces y se conserva la cantidad subradical o base. Los tres radicales tienen índice 2, lo cual haciendo 2 x 2 x 2 nos da 8. La cantidad subradical o base está elevada a 8, entonces tanto el índice (8) como el exponente (8) los dividimos por 8 y queda solo la cantidad subradical o base k.
Simplificar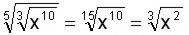
Simplificar
Multiplicamos los índices (5 x 3 = 15) de las raíces y conservamos el exponente (10) de la base (x), luego simplificamos ambos números por 5, que divide tanto a 15 como a 10.
Simplificar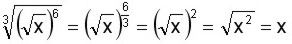 
Expresamos el radical como una potencia con exponente fraccionario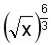 
, luego simplificamos la fracción del exponente y nos queda 
, lo cual es lo mismo que 
donde el exponente 2 de la base se anula con el índice 2 (que no escribe) del radical, para quedar solo x como resultado.
, luego simplificamos la fracción del exponente y nos queda 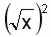, lo cual es lo mismo que 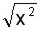donde el exponente 2 de la base se anula con el índice 2 (que no escribe) del radical, para quedar solo x como resultado.
Simplificar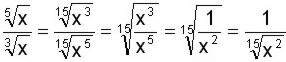 
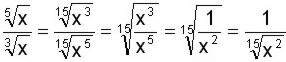
Para dividir (o multiplicar) dos radicales ambos tienen que tener el mismo índice. En este ejemplo no es así, por lo tanto debemos reducir a un índice común, y lo hacemos igual como cuando reducimos fracciones a común denominador.
En este caso, el número o índice común es el 15, el cual dividimos primero por el índice del numerador del radical (15 ÷ 5 = 3) y elevamos la base a ese exponente (3), y luego el 15 lo dividimos por el índice del radical que está como denominador (15 ÷ 3 = 5) y elevamos la base a ese exponente (5) para que la división quede
, con los dos radicales con el mismo índice (15) y se puede realizar la operación.
Simplificar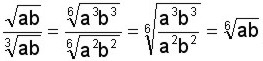 
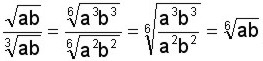
El radical del numerador tiene índice 2 y el radical de denominador tiene índice 3. Para hacer la división debemos igualar los índices. Entre 3 y 2 el índice común es 6, lo aplicamos y operamos igual que el ejemplo anterior.
Simplificar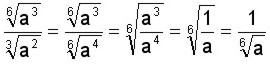 
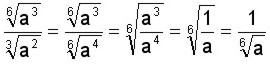
Simplificar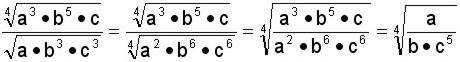 
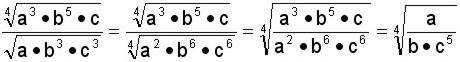
Efectuar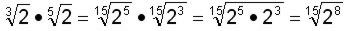 
Sumar y simplificar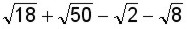 
Debemos recordar que para poder sumar radicales éstos tienen que tener el mismo índice y el mismo radicando. Los radicales del ejemplo tienen el mismo índice pero distinto radicando. Vamos a factorizar los radicandos (o bases) para extraer de cada sumando todos los factores posibles:
Ahora sumamos los coeficientes de cada raíz; o sea, los números que van delante de cada uno de ellos multiplicando:
