Pueden sumarse, restarse, multiplicarse o dividirse si cumplen con determinadas condiciones o reglas.
Suma y resta de radicales
Solamente pueden sumarse (o restarse) dos radicales cuando son radicales semejantes; es decir, si son radicales con el mismo índice e igual radicando (o base subradical).
Producto o multiplicación de radicales
Multiplicar radicales del mismo índice
Se multiplican los radicando (las bases) y se conserva el índice
Multiplicar radicales de distinto índice:
Primero se reducen a índice común y luego se multiplican.
Cociente o división de radicales
Dividir radicales del mismo índice
Se dividen los radicando (las bases) y se conserva el índice
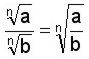
Dividir radicales de distinto índice:
Primero se reducen a índice común y luego se dividen.
Potencia de radicales
Raíz de un radical
Para calcular la raíz de una raíz se multiplican los índices de las raíces y se conserva la cantidad subradical.
Ejemplo:
Racionalizar
Consiste en quitar los radicales del denominador , lo cual facilita el cálculo de operaciones como la suma de fracciones.
Podemos distinguir tres casos, para eliminar los radicales del denominador.
Podemos distinguir tres casos, para eliminar los radicales del denominador.
a)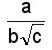 
Se multiplican el numerador y el denominador por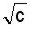 
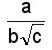Se multiplican el numerador y el denominador por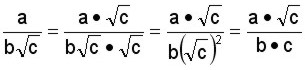 
.
b)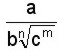
Se multiplican el numerador y el denominador por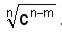 
b)
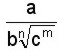Se multiplican el numerador y el denominador por 
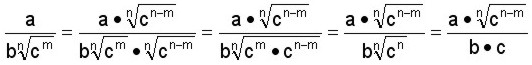.c)
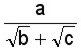
y en general cuando el denominador sea un binomio con al menos un radical, se multiplican el numerador y denominador por el conjugado del denominador. El conjugado es la misma expresión pero con signo contrario.
Además, ver, en Internet:
Ejercicios en
