Para dominarla a cabalidad es necesario conocer en profundidad los instrumentos que utiliza y saber interpretar o leer con exactitud los resultados numéricos que arrojan.
En lo referente a interpretar o leer los resultados numéricos, solo se consigue si dominamos los guarismos del sistema métrico decimal , y si sabemos escribir y leer números decimales .
 |
| Metrología lineal; medir sólidos estáticos. |
Es indudable que en nuestro universo existen distancias lineales siderales, y que en el campo de la astronomía hay unidades e instrumentos apropiados para mensurarlas, pero en nuestro estudio nos referiremos solo a medidas lineales o dimensionales propias de procesos industriales, mecánicos o mineros.
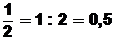
Escribir y leer decimales
A modo de repaso, si se domina la materia, o como estudio necesario si se desconoce, nos detendremos en los números decimales para conseguir una correcta escritura y lectura de los mismos.
 |
| La clave: saber leer e interpretar los decimales. |
Al referirnos a la notación decimal (escritura con números decimales) es necesario empezar por los números fraccionarios (o fracciones).
Una fracción es una relación entre dos números, como, por ejemplo: uno es a dos , que se anota
Lo cual significa que la relación uno es a dos se expresa o se anota como la fracción un medio (1/2), que es igual a 1 (uno) dividido por 2 (dos), lo que arroja como resultado 0,5 (5 décimas).
Como podemos ver, una fracción (o número fraccionario) se puede expresar como fracción o como número decimal .
Los números decimales, entonces, nacen como una forma especial de escritura de las fracciones decimales, de manera que la coma separa la parte entera de la parte decimal.
Un dato importante: Si no hay enteros, se coloca 0 (cero) delante de la coma.
 |
| Un número decimal. |
Analicemos un número decimal :
Todo número decimal se compones de: una parte entera y una parte decimal , separadas por una coma.
Para leer un número decimal hay que hacerlo de acuerdo con la posición de cada dígito en la cifra de que se trate.
La parte entera (antes de la coma) se lee como cualquier número entero:
Veamos los ejemplos en el siguiente cuadro:
|
|
|
|
|
|
|
| ||
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
Una acotación:
Ttodas las cifras del ejemplo indican unidades (o enteros, aunque la palabra se omite), pero, si se fijan, corresponde al “nombre” de la última columna: “unidad” (de izquierda a derecha).
Respecto a la parte decimal, esta se lee también como cualquier número entero, pero ¡OJO! se le agrega un “apellido”; que puede ser “décimas”, “centésimas”, “milésimas”, “diez milésimas”, “cien milésimas”, “millonésimas”, etc.
La clave está en ponerle el “apellido” correcto. Para ello, veamos el siguiente cuadro:
Coma
|
Décimas
|
Centésimas
|
Milésimas
|
Diez milésimas
|
Leemos
|
,
|
0
|
0
|
0
|
4
|
Cuatro diez milésimas
|
,
|
1
|
0
|
7
|
Ciento siete milésimas
| |
,
|
0
|
3
|
Tres centésimas
| ||
,
|
4
|
Cuatro décimas
|
Otra acotación:
Cada cifra decimal (leída como si fuera entero) lleva como “apellido” el nombre de la última columna (desde la coma hacia la derecha).
 |
| Medir la profundidad del desgaste de una pieza. |
Nota: Un número decimal no se altera escribiendo o suprimiendo ceros en su derecha.
Por ejemplo;
8,4 = 8,40 porque la parte entera es la misma y decir 4 décimas es lo mismo que decir 40 centésimas.
3,500 = 3,50 = 3,5 porque no ha variado la parte entera y decir 500 milésimas es lo mismo que 50 centésimas y lo mismo que 5 décimas.
Veamos ahora, algunos ejemplos sobre lectura de decimales:
1.- 9,0004 Se lee: nueve enteros, cuatro diez milésimas
2.- 82,107 Se lee: ochenta y dos enteros, ciento siete milésimas
3.- 354,03 Se lee: trescientos cincuenta y cuatro enteros, tres centésimas
4.- 621,4 Se lee: Seiscientos veintiún enteros, cuatro décimas
5.- 0,9 Se lee: Nueve décimas.
6..- 0,0078 Se lee: Setenta y ocho diez milésimas .
7.- 42,025 Se lee: Cuarenta y dos enteros, veinticinco milésimas
Equivalencia entre pulgada y milímetro
Si ya aprendimos a escribir y leer números decimales, debemos agregar que estos pueden referirse tanto a mediciones expresadas en milímetros como en pulgadas.
En efecto, hay instrumentos que están graduados en pulgadas y en divisores de dicha unidad de medida.
Los decimales se leen exactamente igual, tanto si se refieren a pulgadas como a milímetros, pero hay que entender claramente lo que refleja cada uno.
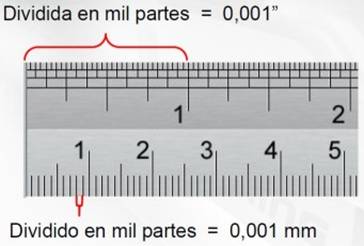 |
En la ilustración de la derecha tenemos una regla graduada en pulgadas (parte de arriba) y en milímetros (parte de abajo)
Para mejor comprensión, cuando se escribe 0,001” (una milésima de pulgada) es que una pulgada se ha dividido en mil partes.
Cuando se escribe 0,001 mm (una milésima de milímetro) es que un milímetro se ha dividido en mil partes.
Para obtener la equivalencia entre una y otra unidad debemos saber que una pulgada equivale a 25,4 milímetros. 1” = 25,4 mm .
Así, para convertir pulgadas en milímetros debemos multiplicar por 25,4 la cantidad de pulgadas y obtenemos la medición en milímetros.
Ejemplo s :
4,5” x 25,4 = 114,3 mm
0,235” x 25,4 = 5,969 mm
Y, de modo inverso, si queremos convertir milímetros en pulgadas, debemos dividir por 25,4 la cantidad de milímetros y obtenemos la medición en pulgadas
Ejemplos:
114,3 mm : 25,4 = 4,5”
5,969 mm : 25,4 = 0,235”
Fuentes Internet:
Ver en I nternet:
Ejercicios sobre lectura de decimales:






